Oblast: Homotetija
Lekcija: Primena sličnosti na pravougli trougao i krug
Razred: 1. razred srednje škole

Primena sličnosti na pravougli trougao

U svakom pravouglom trouglu važi:

• hipotenuzina visina je geometrijska sredina odsečaka koje sama odseca na hipotenuzi;
• kateta je geometrjska sredina hipotenuze i bližeg odsečka hipotenuze;
• trougao ABC je pravougli ako i samo ako je c² = a² + b².

Primena sličnosti na krug

Neka data tačka P u ravni kruga k i neka su a i b dve sečice kruga k  povučene kroz tačku P. Posmatramo tri slučaja, kada je tačka P u krugu, na krugu i van kruga. (Slika 1.)

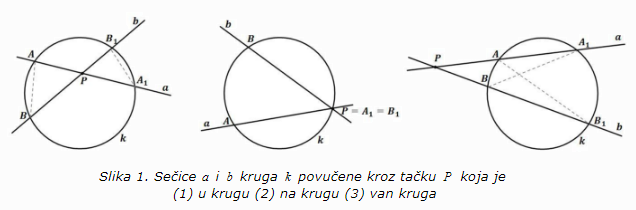
(1) Trouglovi ABP i A₁B₁P su slični jer imaju jednake uglove (kod P i ∠BAP = ∠A₁B₁P). Na osnovu sličnosti sledi AB:BP = B₁P:A₁P  a odatle AP A₁P = BP B₁P.

(2) Kako je A₁P = B₁P=0, tada je AP A₁P= 0 =BP B₁P.

(3) Trouglovi AB₁P i A₁BP imaju zajednički ugao APB i jednake uglove ∠AB₁P = ∠PA₁B, tako da su ta dva trougla slična  i važi PA:PB₁ = PB:PA₁ a odatle PA PA₁ = PB PB₁.

Kada sečica iz P sa krugom k ima zajedničke tačke A i A₁ tada su PA i PA₁ odsečci koje krug k određuje na toj sečici. Sada se može izvesti zaključak na osnovu posmatranih slučajeva.

Ako je k dati krug i P data tačka u ravni kruga k, tada proizvod odsečaka koje krug k određuje na bilo kojoj sečici povučenoj iz tačke P ima konstantan proizvod.

Konstantan proizvod:

p² = PAPA₁

naziva se potencijom tačke P u odnosu na krug k.

Ako je P tačka van kruga k, (u ravni tog kruga) onda je potencija ove tačke u odnosu na krug k jednaka kvadratu odgovarajuće tangentne duži.

Ako je PT tangentna duž i prava a sečica, tada važi:

PT² = PAPA₁ = p²

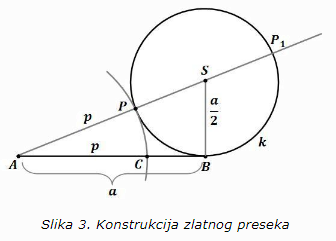
Ako je neka duž AB  tačkom C podeljena tako da je veći odsečak geometrijska sredina duži AB i manjeg odsečka, tj. ako važi AC:AB = BC:AC tada se kaže da je izvršen zlatni presek duži AB. (Slika 2.)

Zlatni presek se konstruiše pomoću potencije tačke A duži AB u odnosu na pogodno izabrani krug. (Slika 3.)

Zadaci i testovi za vežbanje