Oblast: Celi brojevi
Lekcija: Sabiranje i oduzimanje celih brojeva
Razred: 6. razred osnovne škole

Sabiranje celih brojeva

Uvedimo pravila za sabiranje u skupu celih brojeva Z. Neka su m i n prirodni brojevi i m ≥ n, tada važi:

m+ (-n) = m – n
(-n) + m = m – n
(-m) + (-n) = -(m+n)
(-m) + n = – (m-n)
n+ (-m) = -(m-n)

Sabiranje celih brojeva se može prikazati pomoću brojevne prave.

Neka je potrebno sabrati celi broj a čija je koordinata tačka A(a) i pozitivan celi broj b:

Zbir celog broja a i pozitivnog celog broja b je broj jednak koordinati tačke koja se dobija pomeranjem od tačke A(a) za b jediničnih duži u pozitivnom smeru (udesno).

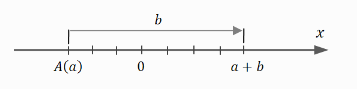Neka je potrebno sabrati celi broj a čija je koordinata tačka A(a) i negativan celi broj b:

Zbir celog broja a i negativnog celog broja b je broj jednak koordinati tačke koja se dobija pomeranjem od tačke A(a) za |b| jediničnih duži u negativnom smeru (ulevo).

• Znak zbira je isti kao znak sabiraka koji ima veću apsolutnu vrednost.
• Ako su sabirci istog znaka, apsolutna vrednost zbira je zbir apsolutnih vrednosti sabiraka.
• Ako su sabirci različitog znaka, apsolutna vrednost zbira je razlika veće i manje apsolutne vrednosti sabiraka.

Oduzimanje celih brojeva

Razlika brojeva a i b je zbir broja a i broja suprotnog broju b:

a-b = a + (-b)

Za sve cele brojeve a i b važi:

b+ (a-b) = b

Svojstva operacije sabiranja

Za svaka tri broja a, b, c∈Z važi:

• ako su a i b celi brojevi onda je i a+b ceo broj;
• a+(-a) = 0, zbir dva suprotna broja je jednak nula;
• a+b = b+a, (svojstvo komutacije);
• a+(b+c) = (a+b)+c, (svojstvo asocijacije).

Zadaci i testovi za vežbanje