Oblast: Geometrija![]()
Lekcija: Podudarnost trouglova
Razred: 1. razred srednje škole
Podudarnost trouglova – Matematika 1. razred srednje škole
Rastojanje između dve tačke A i B se označava sa d(A,B).
Neka su date tačke A,B,C i D, ako je d(A,B)=d(C,D) onda se kaže da su parovi tačaka {A,B} i {C,D} u relaciji podudarnosti, što se zapisuje kao {A,B}≅{C,D}.
Dve duži AB i CD su jednake (podudarne) ako je {AB}≅{CD} što se označava sa:
AB=CD
Izometrijsko preslikavanje (izometrija) je svako obostrano jednoznačno preslikavanje figure F na figuru F1 koje duži preslikava na podudarne duži.
Ako postoji izometrijsko preslikavanje koje figuru F preslikava na figuru F1 tada se kaže da je figura F1 podudarna figuri F, što se označava sa
F≅F1
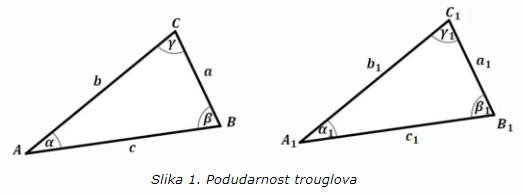
Dakle, dva trougla ABC i A1B1C1 su podudarna ako postoji izometrijsko preslikavanje koje trougao ABC preslikava (prevodi) na trougao A1B1C1, što se označava sa:
△ABC ≅ △A1B1C1
Za dva podudarna trougla važi da su mu sve stranice i svi uglovi jednaki, odnosno:
△ABC≅△A1B1C1 ⇒ AB=A1B1, BC=B1C1, AC=A1C1, α=α1, β=β1, γ=γ1
Prilikom dokazivanja podudarnosti trouglova nije potrebno dokazati jednakost svih stranica i uglova, potrebni i dovoljni uslovi za podudarnost su dati kroz četiri stava.
Stav SSS. Dva trougla su podudarna ako i samo ako su stranice jednog trougla jednake odgovarajućim stranicama drugog trougla:
△ABC≅△A1B1C1 ⇔ a=a1 ∧ b=b1 ∧ c=c1
Stav SUS. Dva trougla su podudarna ako i samo ako su dve stranice jednog trougla i ugao zahvaćen njima jednaki odgovarajućim stranicama i uglu drugog trougla:
△ABC≅△A1B1C1 ⇔ b=b1 ∧ c=c1 ∧ α=α1
Stav USU. Dva trougla su podudarna ako i samo ako imaju jednaku po jednu stranicu i oba odgovarajuća ugla nalegla na tu stranicu:
△ABC≅△A1B1C1 ⇔ c=c1 ∧ α=α1 ∧ β=β1
Stav SSU. Dva trougla su podudarna ako i samo ako su dve stranice i ugao naspram jedne od njih u jednom trouglu jednaki dvema odgovarajućim stranicama i uglu u drugom trouglu, a uglovi naspram druge stranice u oba trougla su iste vrste (oba oštra, oba prava ili oba tupa ugla):
△ABC≅△A1B1C1 ⇔ a=a1 ∧ b=b1 ∧ α=α1 ∧ β i β1 su oba oštri, pravi ili tupi uglovi.
Zadaci i testovi za vežbanje

IMAŠ PROBLEM SA ZADACIMA IZ GEOMETRIJE?
Naruči rešenje zadatka!
Naruči zadatak i u roku od 24h dobijaš rešenje, korak po korak, sa objašnjenjima.
Zadatke rade iskusni profesori matematike.
Naruči svoj zadatak!
ONLINE časovi 1 na 1
Najbolji online časovi u Srbiji.
Preko 1.000 zakazanih časova
godišnje!
Profesori sa iskustvom.
Najbolja usluga.
Zakaži svoj čas!
ONLINE škola matematike
Najsavremenija platforma na ovim prostorima!
Video-lekcije, testovi,
pomoćni materijali, skripte.
Kratki online časovi 1 na 1.
Izveštaj o aktivnostima.