Oblast: Realni brojevi![]()
Lekcija: Rešenje jednačine x² = a (a ≥ 0). Kvadratni koren
Razred: 7. razred osnovne škole
Rešenje jednačine x² = a (a ≥ 0). Kvadratni koren – Matematika za 7. razred
Razmatramo jednačinu oblika x2=a gde je a racionalan broj veći ili jednak nuli, a≥0.
Primer 1. Rešiti jednačinu x2 = 25.
Rešenje: x2 = 25
Rešenje je broj čiji kvadrat iznosi 25:
x = 5 ili x = -5, jer je 52 = 25 i (-5)2 = 25.
Prema tome, jednačina x2 = 25 ima dva rešenja, to su x = 5 i x = -5.
Primer 2. Rešiti jednačinu x2 = 0.
Rešenje: x2 = 0
Zadata jednačina ima samo jedno rešenje:
x = 0, jer je samo 02 = 0.
Na osnovu ovih primera možemo da zaključimo da je uslov a ≥ 0 potreban zbog toga što ne postoji racionalan broj koji podignut na kvadrat daje negativan broj. Drugim rečima, x2 ne može biti negativan broj.
Jednačina x2 = a, a ≥ 0:
- za a>0 ima dva rešenja, to su x = √a i x = -√a,
- za a=0 ima jedno rešenje, to je x = √a = √0 = 0.
Vratimo se na primer 1. Pozitivno rešenje jednačine x2 = 25 (broj 5) naziva se kvadratni koren broja 25, koji zapisujemo na sledeći način:
√25
(čita se: “kvadratni koren od 25”)
gde je simbol √2 oznaka kvadratnog korena, a broj 25 potkorena veličina.
Dakle, rešenja jednačine x2 = 25 su:
x = √25 = 5 i x = -√25 = -5.
Rešenje jednačine (primer 2) x2 = 0 je:
x = √0 = 0.
Neka je a nenegativan broj, tj. neka je a ≥ 0. Kvadratni koren od broja a, u oznaci a, je takođe nenegativan broj čiji je kvadrat jednak broju a.
(√a)2=a, a≥0.
Potkorena veličina mora biti nenegativna, jer kvadratni koren iz negativnog broja nije definisan u skupu racionalnih brojeva Q.
Primer 3. Izračunati:
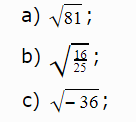
Rešenje:

Zadaci i testovi za vežbanje

IMAŠ PROBLEM SA REALNIM BROJEVIMA?
Naruči rešenje zadatka!
Naruči zadatak i u roku od 24h dobijaš rešenje, korak po korak, sa objašnjenjima.
Zadatke rade iskusni profesori matematike.
Naruči svoj zadatak!
ONLINE časovi 1 na 1
Najbolji online časovi u Srbiji.
Preko 1.000 zakazanih časova
godišnje!
Profesori sa iskustvom.
Najbolja usluga.
Zakaži svoj čas!
ONLINE škola matematike
Najsavremenija platforma na ovim prostorima!
Video-lekcije, testovi,
pomoćni materijali, skripte.
Kratki online časovi 1 na 1.
Izveštaj o aktivnostima.