Oblast: Realni brojevi![]()
Lekcija: Realni brojevi. Jednakost √a² = |a|
Razred: 7. razred osnovne škole
Realni brojevi. Jednakost √a² = |a| – Matematika za 7. razred
Realne brojeve predstavljaju svi racionalni i iracionalni brojevi. O iracionalnim brojevima ćemo govoriti u narednoj lekciji, za sada naglasimo da je skup realnih brojeva širi skup od skupa racionalnih brojeva, što znači da su svi racionalni brojevi sadržani u skupu realnih brojeva.
U predhodnoj lekciji smo naučili da potkorena veličina kvadratnog korena mora biti nenegativan broj jer u suprotnom (ako je negativan) kvadratni koren nije definisan. Takođe i vrednost kvadratnog korena je nenegativan broj. Dalje, pogledajmo kako se izračunava kvadratni koren kada je potkorena veličina kvadrat nekog broja a. Razmatramo tri slučaja kada je a>0, a=0 i a<0.
1° Kvadratni koren iz kvadrata pozitivnog broja
Primer 1. Izračunati
![]()
Rešenje:
![]()
U ovom primeru smo izračunali kvadratni koren iz kvadrata pozitivnog broja (7) i dobili rezultat koji je jednak tom pozitivnom broju.
![]()
2° Kvadratni koren iz kvadrata broja koji je jednak nuli.
Primer 2. Izračunati:
![]()
Rešenje:
![]()
Kvadratni koren iz kvadrata nule je jednak nula.
![]()
3° Kvadratni koren iz kvadrata broja koji je manji od nule.
Primer 3. Izračunati:
![]()
Rešenje:
![]()
Broj -7 podignut na kvadrat daje pozitivan broj, što znači da je potkorena veličina pozitivan broj pa je i u ovom slučaju kvadratni koren definisan. Kvadratni koren iz kvadrata negativnog broja je jednak njegovom suprotnom broju (broju -7 kada ispred njega dodamo znak minus) a to je pozitivan broj.
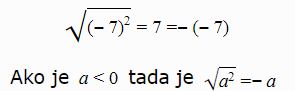
U sva tri slučaja smo dobili nenegativne rezultate. Zaključujemo da je kvadratni koren iz kvadrata nekog broja a jednak njegovoj apsolutnoj vrednosti.
Za svaki racionalan broj a važi:
![]()
Zadaci i testovi za vežbanje

IMAŠ PROBLEM SA REALNIM BROJEVIMA?
Naruči rešenje zadatka!
Naruči zadatak i u roku od 24h dobijaš rešenje, korak po korak, sa objašnjenjima.
Zadatke rade iskusni profesori matematike.
Naruči svoj zadatak!
ONLINE časovi 1 na 1
Najbolji online časovi u Srbiji.
Preko 1.000 zakazanih časova
godišnje!
Profesori sa iskustvom.
Najbolja usluga.
Zakaži svoj čas!
ONLINE škola matematike
Najsavremenija platforma na ovim prostorima!
Video-lekcije, testovi,
pomoćni materijali, skripte.
Kratki online časovi 1 na 1.
Izveštaj o aktivnostima.