Oblast: Sličnost trouglova![]()
Lekcija: Primena sličnosti na pravougli trougao
Razred: 8. razred osnovne škole
Primena sličnosti na pravougli trougao – Matematika za 8. razred
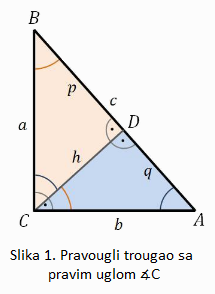
Posmatramo pravougli trougao ABC prikazan na slici 1. Visina h iz temena C deli pravugli trougao ABC na dva pravougla trougla DBC i ADC, a podnožje visine, tačka D deli hipotenuzu na dva odsečka p i q. Trouglovi DBC i ADC su slični trouglu ABC jer imaju po jedan prav ugao i jedan zajednički oštar ugao sa trouglom ABC (prvi stav sličnosti-UU). Pored slike su date relacije koje važe za uglove sva tri pravougla trougla.
∆ABC:
∡C=90°,
∡A+∡B+∡C=180°,
∡A+∡B+90°=180°,
∡A+∡B=90°,
∡A=90°-∡B,
∡B=90°-∡A.
∆DBC:
∡D=90°,
∡B=∡B (∆ABC),
∡C=90°-∡B=∡A (∆ABC).
∆ADC:
∡D=90°,
∡A=∡A (∆ABC),
∡C=90°-∡A=∡B (∆ABC).
Na osnovu sličnosti trouglova ∆ABC~∆DBC sledi:
a:b:c=p:h:a,
(kada formiramo predhodnu proporciju vodimo računa o tome da se odgovarajuće stranice sličnih trouglova nalaze naspram odgovarajućih jednakih uglova)
![]()
Odavde se dobija:
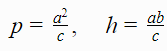
Na osnovu sličnosti trouglova ∆ABC~∆ADC sledi:
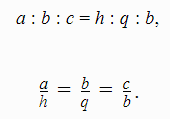
Odavde se može izraziti odsečak q:
![]()
Kada izraze za p i q pomnožimo, dobija se:
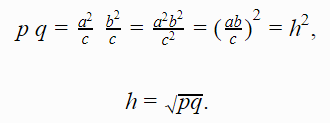
Prema tome, visina hipotenuze je geometrijska sredina odsečaka p i q.
Kada izraze za p i q saberemo, dobija se:
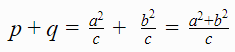
na slici se vidi da takođe važi i
p+q=c,
pa imamo:
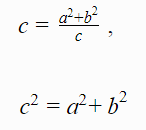
i na ovaj način je dokazana već poznata Pitagorina teorema.
Zadaci i testovi za vežbanje

IMAŠ PROBLEM SA ZADACIMA IZ SLIČNOSTI TROUGLOVA?
Naruči rešenje zadatka!
Naruči zadatak i u roku od 24h dobijaš rešenje, korak po korak, sa objašnjenjima.
Zadatke rade iskusni profesori matematike.
Naruči svoj zadatak!
ONLINE časovi 1 na 1
Najbolji online časovi u Srbiji.
Preko 1.000 zakazanih časova
godišnje!
Profesori sa iskustvom.
Najbolja usluga.
Zakaži svoj čas!
ONLINE škola matematike
Najsavremenija platforma na ovim prostorima!
Video-lekcije, testovi,
pomoćni materijali, skripte.
Kratki online časovi 1 na 1.
Izveštaj o aktivnostima.