Oblast: Piramida
Lekcija: Zpremina piramide
Razred: 8. razred osnovne škole

Kavalijerijev princip glasi:

Ako se dva tela preseku paralelnim ravnima i ako pri tome preseci tela sa bilo kojom od tih ravni imaju jednake površine, tada ta dve tela imaju jednake zapremine.

Neka su date dve četvorostrane prizme jednakih visina i jednakih površina osnova koje leže u ravni α. Ako se obe prizme preseku sa ravni  β paralelnoj sa ravni α dobijaju se preseci podudarni sa odgovarajućim osnovama prizmi, to znači da i preseci imaju jednake površine. Prema Kavalijerijevom principu sledi da obe prizme imaju jednake zapremine. (Slika 1.)

Dakle, dve prizme koje imaju jednake visine i  jednake površine baza, imaju jednake zapremine.

Neka su date dve četvorostrane piramide jednakih visina i jednakih površina osnova koje leže u ravni α. Ako se obe piramide preseku sa ravni  β paralelnoj sa ravni α dobijaju se preseci slični sa odgovarajućim osnovama. Koeficijenti sličnosti osnove i preseka kod obe piramide su jednaki jer je koeficijent sličnosti jednak razmeri rastojanja ravni α i β od vrhova piramida. Kako je odnos površina sličnih figura jednak kvadratu koeficijenta sličnosti, to znači da preseci obe piramide imaju jednake površine.

Prema Kavalijerijevom principu sledi da obe piramide imaju jednake zapremine. (Slika 2.)

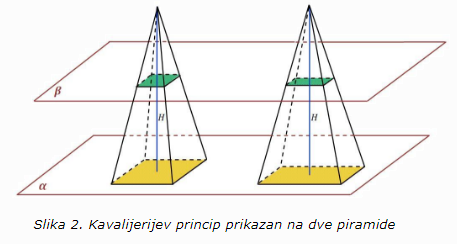
Dakle, dve piramide jednakih visina i jednakih površina osnova, imaju jednake zapremine.

Posmatramo sliku 3. na kojoj je prikazana prizma ABCDEF. Presecanjem prizme ravnima ACF i ECF dobijaju se tri piramide koje imaju  zajednički vrh F. To su piramide FABC, FEAC i FECD  (piramide se označavaju navođenjem svih temena, gde je prvo teme vrh piramide). Sve tri piramide su zbog lakšeg uočavanja prikazane razdvojeno na desnoj strani slike.

Piramide FEAC i FECD imaju jednake površine baza, jer su trouglovi EAC i ECD podudarni. Takođe, obe ove piramide imaju jednake visine jer im je zajednički vrh F. Kako su površine osnova i visine ovih dveju piramida jednake, po Kavalijerovom principu sledi  da one imaju i jednake zapremine.

Piramide FABC i CEFD (piramidu FECD posmtramo kao da joj je vrh u temenu C) imaju jednake površine baza, jer su trouglovi ABC i EFD podudarni. Visine ovih piramida su takođe jednake jer su one ujedno i visine (dužine bočnih ivica) date prizme. Prema Kavalijerovom principu sledi  da ove dve piramide imaju i jednake zapremine.

Zaključujemo da sve tri piramide FEAC, FECD i FABC imaju jednake zapremine.

V(FEAC) = V(FECD) = V(FABC)

Zapremina prizme ABCDEF je kao što znamo BH, što znači da je:

¹/₃BH = V(FEAC) = V(FECD) = V(FABC)

Zapremina piramide je jednaka trećini zapremine prizme koja sa tom piramidom ima podudarnu osnovu i jednaku visinu. To znači da se zapremina svake piramide računa po formuli:

gde je:

• B – površina osnove (baze) piramide,
• H – visina piramide,
• V – zapremina piramide.

Zadaci i testovi za vežbanje