Oblast: Linearna funkcija
Lekcija: Crtanje i čitanje grafika linearne funkcije
Razred: 8. razred osnovne škole

U predhodnim lekcijma videli smo da je grafik linearne funkcije prava. S obzirom da je svaka prava određena sa dve tačke, to znači da je za crtanje grafika linearne funkcije potrebno uneti dve tačke u koordinatnu ravan Oxy i konstruisati pravu liniju. Skiciranje grafika linearne funkcije pokazaćemo na sledećem primeru.

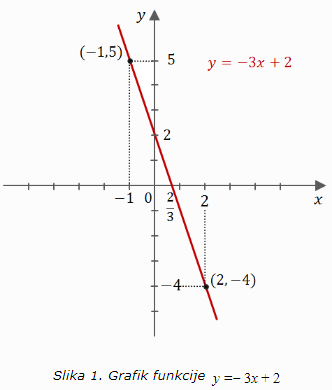
Primer 1: Zadata je funkcija y = -3x+2. Nacrtati grafik funkcije.

Domen ove linearne funkcije nije zadan, pa uzimamo da je domen ceo skup R. To znači da  za crtanje grafika funkcije možemo proizvoljno izabrati dve vrednosti nezavisno promenljive x  za koje računamo vrednost funkcije. Formiramo tabelu, u prvoj vrsti upisujemo izabrene vrednosti nezavisno promenljive x, a u drugoj vrsti izračunate vrednosti funkcije.

y = -3x+2,    y(-1) = -3(-1)+2 = 5,     y(2) = -3(2)+2 = -4.

Uređeni par (x,y) predstavlja jednu tačku u koordinatnoj ravni Oxy. Dakle, u koordinatnu ravan unosimo tačke (-1,5) i (2,-4) i skiciramo grafik zadate funkcije. (Slika 1.)

Prilikom formiranja tabele mogu se uzeti i više od dve vrednosti nezavisno promenljive. Tako dobijamo više tačaka u kooridantnoj ravni i veću sigurnost prilikom crtanja grafika, jer ukoliko bi npr. pogrešno izračunali vrednost funkcije za neku promenljivu x, ta tačka ne bi pripadala pravoj koja predstavlja grafik zadate funkcije.

Ispravnost nacrtanog grafika možemo proveriti izračunavanjem nule funkcije:

-3x + 2 = 0

-3x = -2

x = ²/₃

Tačka preseka grafika funkcije i x-ose (²/₃, 0) što se može videti na grafiku. Tačka preseka grafika funkcije i y-ose je jednaka vrednosti funkcije kada je x=0.

y = -3x+2
y = -3(0)+2=2

Dakle, tačka preseka grafika funkcije i y-ose je (0, 2) što se takođe može videti na grafiku.

Dalje možemo da ispitamo znak funkcije, pri čemu određujemo:

• za koje vrednosti x je linearna funkcija pozitivna (veća od nule), y>0;
• za koje vrednosti x je linearna funkcija negativna (manja od nule), y<0.

Ispitujemo za koje vrednosti x je funkcija y = -3x+2 veća od nule (y>0).

Rešavamo linearnu nejednačinu:

-3x+2 > 0

-3x > -2

3x < 2

x < 23

Funkcija je pozitivna, tj.  y > 0 za x < ²/₃.

Zatim, ispitujemo za koje vrednosti x je funkcija y = -3x+2 manja od nule (y<0).

Rešavamo linearnu nejednačinu:

-3x+2 < 0

-3x < -2

3x > 2

x > ²/₃

Funkcija je negativna, tj.  y < 0 za x > ²/₃.

Znak funkcije se može pročitati i sa grafika funkcije.

• Funkcija je pozitivna u onim tačkama grafika funkcije koje se nalaze iznad x-ose,
• Funkcija je negativna u onim tačkama grafika funkcije koje se nalaze ispod x-ose.

Posmatramo grafik funkcije (Slika 1.)

• za x < ²/₃ grafik funkcije (prava) nalazi se iznad x-ose, dakle za  x < ²/₃ funkcija je pozitivna,
• za x > ²/₃ grafik funkcije (prava) nalazi se ispod x-ose, dakle za  x > ²/₃ funkcija je negativna.

Zadaci i testovi za vežbanje