Oblast: Racionalni algebarski izrazi
Lekcija: Polinomi, sređen oblik polinoma, sabiranje, oduzimanje, množenje polinoma
Razred: 1. razred srednje škole

Algebarski izrazi su izrazi formirani od konstanti i promenljivih koje su međusobno povezane algebarskim operacijama kao što su sabiranje, oduzimanje, množenje,deljenje,stepenovanje i korenovanje. U nastavku razmatramo racionalne algebarske izraze.

1. Simboli realnih brojeva (4,0,-3, 1/7 ,√2,e…) su racionalni algebarski izrazi;
2. Simboli promenljivih (x,y,z,a,b,α,β…) su racionalni algebarski izrazi;
3. Ako su A i B racionalni algebarski izrazi, onda su i (A+B),  (A-B),  AB,  A/B racionalni algebarski izrazi;
4. Svi racionalni algebarski izrazi se dobijaju primenom prva tri pravila.

Za razliku od algebarskih izraza, pri formiranju racionalnih algebarskih izraza ne učestvuje operacija korenovanja, tačnije korenovanje se može primeniti samo na konstante.

Prema tome, racionalne algebarske operacije su: sabiranje, oduzimanje, množenje (što podrazumeva i stepenovanje) i deljenje.

Polinomi su celi racionalni algebarski izrazi, tj. izrazi u čijem formiranju ne učestvuje operacija deljenja – izrazom koji sadrži promenljive.

Polinom se sastoji od monoma za koje se kaže da su gradivni elementi polinoma. Primeri monoma su:

Kanonski oblik polinoma je izraz:

P(x) = a_nxⁿ + a_n-1 x^n-1 + … a₁x + a₀,    gde je

• x – promenljiva;
• a₀, a₁, … a_n  – realni brojevi, konstante ili koeficijenti polinoma;
• n – prirodan broj ili nula.

Ako je a_n≠0, onda se kaže da je taj polinom n-tog stepena, a koeficijent a_n predstavlja najstariji koeficijent polinoma.

Pod polinomom nultog stepena podrazumeva se konstanta različita od nule, P=a₀, a₀≠0.

Srediti polinom znači dovesti ga u kanonski oblik.

Predhodni izraz predstavlja polinom jedne promenljive. Oznaka P(x) pokazuje da se radi o izrazu koji zavisi od promenljive x. To znači da svaki polinom definiše jednu funkciju.

Vrednost polinoma u nekoj tački skupa R se računa na sledeći način:

P(x) = 2x³-5x²+3x+7

P(2) = 22³-52²+32+7 = 16-20+6+7=9

Dva polinoma P i Q su jednaki ako imaju ako imaju jednake stepene i sve odgovarajuće koeficijente:

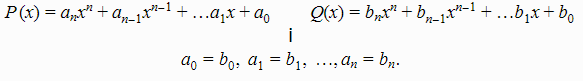
• Zbir dva polinoma P(x) i Q(x) je polinom P(x)+Q(x).
• Razlika dva polinoma P(x) i Q(x) je polinom P(x)-Q(x).
• Proizvod dva polinoma P i Q je polinom P(x)Q(x).

Zadaci i testovi za vežbanje