Oblast: Pitagorina teorema
Lekcija: Primena Pitagorine teoreme na jednakokraki i pravougli trapez
Razred: 7. razred osnovne škole

Posmatramo jednakokraki trapez  ABCD osnovica a i b i krakova c. (Slika 1.) Visina trapeza je rastojanje između osnovica. Visina h spuštena iz temena C i D na osnovicu a određuje dva podudarna pravougla trougla. Jedan od tih trouglova je trougao AED. Njegova hipotenuza je krak c, jedna kateta je visina h. Potrebno je još odrediti i dužinu druge katete (dužinu duži AE).

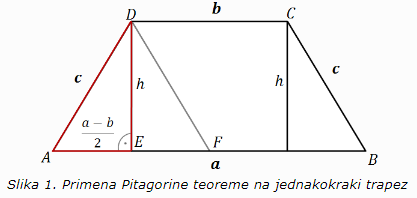
Ako iz temena D povučemo duž, paralelnu sa krakom BC, dobićemo jednakokraki trougao AFD. Dužina duži AF koja predstavlja osnovicu jednakokrakog trougla je a – b, tj. AF = a-b. To onda znači da je dužina duži AE =

jer je to polovina osnovice jednakokrakog trougla. Na osnovu Pitagorine teoreme dobijamo:

Posmatramo pravougli trapez  ABCD osnovica a i b i krakova c₁ i c₂. (Slika 2.) Kraći krak c₁ je ujedno visina trapeza h. Visina h spuštena iz temena C na osnovicu a određuje pravougli trougao EBC. Njegova hipotenuza je krak c₂. Jedna kateta je visina h, druga kateta je duž EB koja je jednaka a-b tj. EB = a-b.

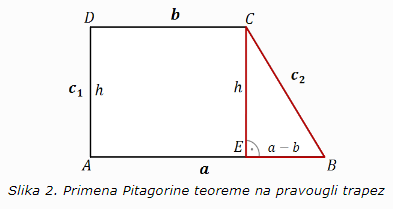
Na osnovu Pitagorine teoreme sledi:   c₂² = (a-b)² + h².

Zadaci i testovi za vežbanje