Oblast: Celi brojevi
Lekcija: Skup celih brojeva
Razred: 6. razred osnovne škole

Prirodni brojevi su brojevi: 1, 2, 3, 4, 5 …. Skup prirodnih brojeva označavamo velikim slovom N i zapisujemo:

N = {1, 2, 3, 4, 5, 6,…}

Ako skupu prirodnih brojeva dodamo broj 0 dobijamo skup prirodnih brojeva i nule koji označava sa:

Dalje razmatramo proširenje ovog skupa” sa negativnim celim brojevima. Negativan celi broj je broj koji nastaje kada se prirodnom broju pridruži znak ”-” (minus). Npr. kada prirodnom broju 10 pridružimo znak ”-” dobijamo negativan celi broj -10.

Prema tome, negativni celi brojevi su -1, -2, -3, -4, -5, …

Ako skup prirodnih brojeva i nule proširimo sa negativnim celim brojevima dobijamo skup celih brojeva koji se koji označava sa Z i zapisuje:

Šta čini skup celih brojeva?

Skup celih brojeva čine:

• negativni celi brojevi,
• nula i
• pozitivni celi brojevi.

Skup negativnih celih brojeva označavamo sa:

Skup pozitivnih celih brojeva označavamo sa:

Vidimo da je skup pozitivnih celih brojeva jednak skupu prirodnih brojeva:

Prirodnim brojevima se može pridružiti znak ”+”. Broj 1 se može zapisati kao  +1, broj 2 kao +2,… jer je 1=+1,  2=+2… Tako smo dobili da svaki celi broj osim nule ima znak. Prirodni brojevi se još nazivaju i pozitivni celi brojevi.

Brojevna prava

Prirodni brojevi i nula se prikazuju na brojevnoj polupravoj. Početna tačka na polupravoj je tačka O kojoj pridružujemo broj 0. Tačka O se naziva koordinatni početak. Biramo sledeću tačku na brojevnoj polupravoj, to je tačka A kojoj pridružujemo broj 1.

Duž OA se naziva jedinična duž. Ako je n bilo koji prirodan broj, nanoseći jediničnu duž od koordinatnog početka n puta dolazimo do tačke N koja određuje taj broj n. Na taj način je svakom prirodnom broju pridružena po jedna tačka na brojevnoj polupravoj.

Slika 1. Brojevna poluprava

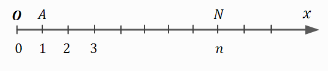
Da bi smo prikazali sve cele brojeve, potrebna nam je prava koju dobijamo tako što ćemo brojevnu polupravu Ox produžiti levo od koordinatnog početka. Jedinične duži nanosimo od koordinatnog početka ulevo. Krajevima tih jediničnih duži pridružujemo brojeve -1,-2,… Ako levo od tačke O nanesemo n puta jediničnu duž dobijamo tačku kojoj odgovara broj -n.

Slika 2. Brojevna prava

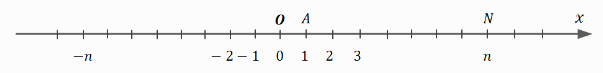
Pravu x na kojoj su pridruženi celi brojevi nazivamo brojevna prava. Tačka O je koordinatni početak. Svakom celom broj n odgovara tačno jedna tačka N brojevne prave. Broj n je koordinata tačke N koju zapisujemo kao N(n).

Zadaci i testovi za vežbanje